深入理解树状数组

1. lowbit
2. 树状数组区间查询
3. 树状数组单点修改
4. 区间修改树状数组

我的上一篇博客介绍了树状数组的用法。虽然靠上一篇博客的知识已经能解不少题了，但是很多稍微上难度的题都需要对树状数组进行一定程度上的“魔改”才能解决，光是将树状数组作为黑盒使用肯定不行。

lowbit

先谈一个稍微轻松一点的话题：为什么lowbit(x) = x & -x？

众所周知，数值在计算机中以补码的形式储存。如果不知道什么是补码，可以先上网搜索相关资料。

一个正数的补码在数字上就是它的二进制表示。比如十的二进制表示为1010，十的32位补码就为

1

00000000000000000000000000001010

其中，最左边的0不表示数字，而是相当于正号，表示这是个正数。

负数的补码相当于它的相反数的补码-1之后，再将这个补码的每一位取反。比如，为了求负十的补码，我们将上面十的补码减上一，得到

1

00000000000000000000000000001001

之后再将这一串编码取反，得到

1

11111111111111111111111111110110

这就是负十的补码了。同样，最左边的那一位是符号位，为1表示这是个负数。

试着将这两个补码相加，可以发现会一直进位直到溢出（即不存在的“第33位”变成1），原来的32位全部变成了0。通过这种别扭的方式求出补码，也就是为了使一个数的补码与它的相反数的补码相加后能通过进位与溢出得到0，方便在计算机中进行各种运算。

既然这两个补码是相加到溢出变成0，那么它们一定满足：最低位的1都为1，其它位要么都为0，要么相反。否则就不能满足相加等于0。而满足了上面的性质，将两个补码按位与，自然就只有最低位的1取1，其它位都取0，也就得到了lowbit。

假设有一个数列a[]，以它为基础建成一个树状数组c[]，c[x]就表示：在数列a[]上，以i为右端点，长度为lowbit(x)的子段所有元素之和，即

$\sum^{x}_{i=x-lowbit(x)+1}a[i]$

这张图描绘了树状数组建成后的模样。

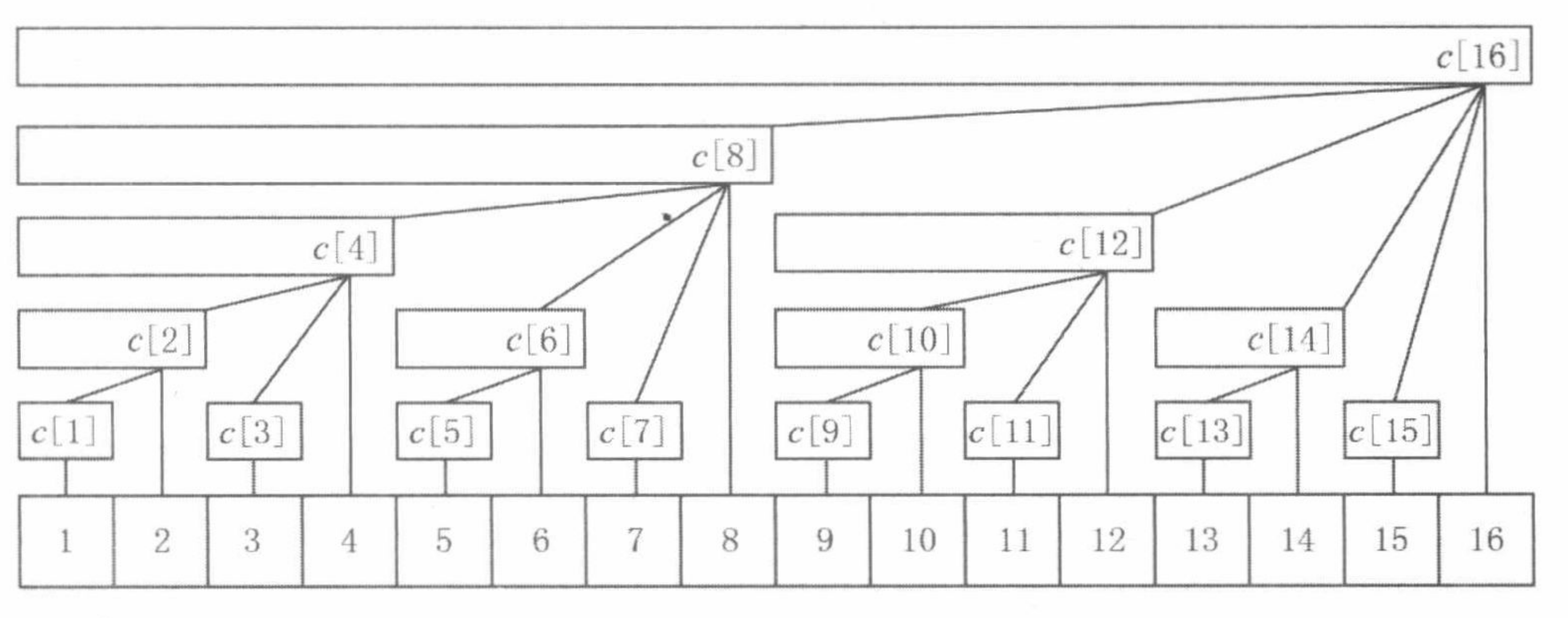
树状数组区间查询

上一篇博客提到，树状数组能求出某个位置的前缀和，并通过前缀和得到任意区间的值（如果不知道什么是前缀和请自行查阅其他资料）。通过树状数组求前缀和的代码如下

1
2
3
4
5
6
7
8
9
10

int sum(int x, int *c) //求x处的前缀和
{
    int ret = 0;
    while (x > 0)
    {
        ret += c[x];
        x -= lowbit(x);
    }
    return ret;
}

是如何通过这一串代码求得x处的前缀和的？

已知：c[x]表示在数列a[]上，以x为右端点，长度为lowbit(x)的子段所有元素之和。

在上面的代码中，之所以屡次执行x -= lowbit(x)，是因为这一步上面的ret += c[x]已经将x前面的lowbit(x) - 1个元素的和都统计过了，不需再重复统计。所以只需要一直执行这两步，就可以得到x处的前缀和了。

在这里，lowbit的作用就体现了出来：随着循环的进行，lowbit(x)是一直增大的，每一次至少都会翻一倍（具体可以对照上面的图执行这些代码来试试看）。lowbit实质上是用一种类似倍增的思想，在不重不漏的情况下，保证了能以$O(logn)$回答对前缀和的询问。

树状数组单点修改

上一篇博客给出了树状数组单点修改的代码

1
2
3
4
5
6
7
8

void point_add(int num, int x, int *c) //将序列的第num个元素加上x
{
    while (num <= n) //n:序列的总长度
    {
        c[num] += x;
        num += lowbit(num);
    }
}

当a[num]的值变化时，c[]中所有含有a[num]这个元素的树状数组“结点”都得做出相应的变化。由于c[num]表示在数列a[]上，以x为右端点，长度为lowbit(num)的子段所有元素之和，c[num]当然是要变化的。

其它需要变化的“结点”呢？根据上面的那张图不难发现：c[num]在树状数组中的“父节点”是c[num + lowbit(num)]。只需要将c[num]的父节点、父节点的父节点、父节点的父节点的父节点…的值全部改变，c[]中所有含有a[num]这个元素的树状数组“结点”就都相应地变化了。

接下来回答这个问题：为什么c[num]在树状数组中的“父节点”是c[num + lowbit(num)]？还是以数字十为例，它的二进制表示是

1

1010

lowbit(10)是

1

0010

将这两个数相加，就得到了

1

1100 = 12

观察上面的过程。首先，一个数与它的lowbit相加必然在最低位产生进位，这使得它加上自己的lowbit所新产生的数的低位不再有1，导致新数的lowbit增大；由于c[num]表示在数列a[]上，以x为右端点，长度为lowbit(num)的子段所有元素之和，lowbit增大实质上就是“结点”所覆盖区间的范围增大，对照上面那张图，就是结点的深度减少。同时，在树状数组中，父节点的编号值一定大于任意子节点的编号值。在深度更浅的点中，无法找到编号值大于num，且编号值与num的差值比num + lowbit(num)更小的点了。因此c[num]的父节点就是c[num + lowbit(num)]。

区间修改树状数组

之所以是“区间修改树状数组”而不是“树状数组区间修改”，是因为若想高效实现区间修改，需要两个树状数组联动。区间修改树状数组实际上可以看作是基于树状数组实现的另一种数据结构了。

构造这样的一个数组b[]。初始状态下，b的每一项都是0。当需要将原序列的区间[l, r]中的各个元素都加上一个数x时，对b数组进行如下操作

1
2

b[l] += x;
b[r + 1] -= x;

设b数组的前缀和为s[]经过这样的操作之后，s的变化如下：

• s[1]、s[2]、s[3]、...、s[l-1]：不变
• s[l]、s[l+1]、s[l+2]、...、s[r]：增加x
• s[r+1]、s[r+2]、s[r+3]...：不变

不难发现，这基本满足了区间修改的要求。通过s的前缀和（即b数组的前缀和的前缀和）就可以求出各个子区间变化的值了。

例如下面这个数列a

1

1 1 1 1 1

它对应的数组b在初始状态下为

1

0 0 0 0 0

b的前缀和s在初始状态下为

1

0 0 0 0 0

接下来需要进行如下操作：将a的[2, 4]区间上每一个数都加上2。根据上面所说的，就是将b[2]加上2，b[5]减去2。b数组就变成

1

0 2 0 0 -2

b的前缀和s就变成了

1

0 2 2 2 0

接下来询问a的[1, 4]子段上所有元素之和。这个字段和由两个部分组成，一部分是a原本的值，即a[1]+a[2]+a[3]+a[4]=4，这个值可以通过a的前缀和求出来；另一部分就是后续更改的值，也就是刚刚的“将a的[2, 4]区间上每一个数都加上2”。这一部分的值就是相应区间的s的区间和，即s[1]+s[2]+s[3]+s[4]=6可以通过s的前缀和求出来。更改后的a的[1, 4]子段上所有元素之和就是6+4=10。

也就是说，经过若干次修改后，原数组在x位置的前缀和增加的值为

$\sum_{i=1}^{x}s[i]$

其中$s[i]=\sum_{j=1}^{i}b[i]$，故原式等于

$\sum_{i=1}^{x} \sum_{j=1}^{i}b[i]$

将该式展开，并统计$b[]$的每一项出现的次数，得

$x \times b[1] \\ +(x-1) \times b[2] \\ +(x-2) \times b[3] \\ +... \\ +(x-x+1) \times b[x]$

即

$\sum_{i=1}^{x}((x-i+1) \times b[i]) \\ =\sum_{i=1}^{x}((x+1)b[i] - i \times b[i]) \\ =(x+1) \times \sum_{i=1}^xb[i] - \sum_{i=1}^{x}(i \times b[i])$

最终的这个式子，可以通过$i \times b[i]$的前缀和和$b[i]$的前缀和得到。维护两个它们两个的树状数组，就可以快速得到它们的前缀和了。假设$b[i]$对应的树状数组是$bit[0][i]$，$i \times b[i]$对应的树状数组是$bit[1][i]$。每次区间修改将区间[l, r]中的所有元素加上x的操作如下：

• 通过$bit[0][]$单点修改，使b[l] += x, b[r+1] -= x
• 通过$bit[1][]$单点修改，使l*b[l] += l*x, (r+1)*b[r+1] -= (r+1)*x（因为每当$b[i]$增加x，$i \times b[i]$的值增加$i\times x$）。

通过两个树状数组实现区间修改的代码就如下

1
2
3
4
5
6
7

void internal_add(int l, int r, long long x)
{
    add(0, x, l);// 第一个参数为0表示修改b[i]对应树状数组，为1表示修改i*b[i]对应树状数组
    add(0, -x, r + 1);
    add(1, l * x, l);
    add(1, -x * (r + 1), r + 1);
}

前面我们已经求出原序列上变化的值的前缀和化出来的最终表达式$=(x+1) \times \sum_{i=1}^xb[i] - \sum_{i=1}^{x}(i \times b[i])$。通过通过对两个树状数组调用sum()函数，我们可以得到$b[]$和$i \times b[]$的前缀和，通过前缀和之差就能得到序列任意区间的变化值了。

1
2
3
4

long long internal_query(int l, int r)// 求区间[l, r]的变化值
{
    return (r + 1) * sum(0, r) - l * sum(0, l - 1) - (sum(1, r) - sum(1, l - 1));
}

针对模板题给出使用例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <cctype>
#include <iomanip>
long long bit[2][100005], a[100005];
int n;
int lowbit(int x)
{
    return x & -x;
}
void add(int it, int x, int num)
{
    while (num <= n)
    {
        bit[it][num] += x;
        num += lowbit(num);
    }
}
long long sum(int it, int num)
{
    long long ret = 0;
    while (num > 0)
    {
        ret += bit[it][num];
        num -= lowbit(num);
    }
    return ret;
}
void internal_add(int l, int r, long long x)
{
    add(0, x, l);
    add(0, -x, r + 1);
    add(1, l * x, l);
    add(1, -x * (r + 1), r + 1);
}
long long internal_query(int l, int r)
{
    return (r + 1) * sum(0, r) - l * sum(0, l - 1) - (sum(1, r) - sum(1, l - 1));
}
using namespace std;
int main()
{
    int q, i, l, r;
    long long x;
    char o[5];
    scanf("%d%d", &n, &q);
    for (i = 1; i <= n; i++)
    {
        scanf("%lld", &a[i]);
        a[i] += a[i - 1];//树状数组只能维护区间的变化值，想要得到实际的值需要加上区间的原值，因此用到原序列前缀和
    }
    while (q--)
    {
        scanf("%s", o);
        if (o[0] == 'Q')
        {
            scanf("%d%d", &l, &r);
            printf("%lld\n", a[r] - a[l - 1] + internal_query(l, r));//原序列区间值加上变化值
            continue;
        }
        scanf("%d%d%lld", &l, &r, &x);
        internal_add(l, r, x);
    }
    return 0;
}